- What is electricity?
- Resistance, Conductance & Ohms Law
- Practical Resistors
- Power and Joules Law
- Maximum Power Transfer Theorem
- Series Resistors and Voltage Dividers
- Kirchhoff’s Voltage Law (KVL)
- Parallel Resistors and Current Dividers
- Kirchhoff’s Current Law (KCL)
- Δ to Y Network Conversion
- Y to Δ Network Conversion
- Voltage and Current Sources
- Thevenin’s Theorem
- Norton’s Theorem
- Millman’s Theorem
- Superposition Theorem
- Mesh Current Analysis
- Nodal Analysis
- Capacitance
- Series & Parallel Capacitors
- Practical Capacitors
- Inductors
- Series & Parallel Inductors
- Practical Inductors
Like Kirchhoff’s Voltage Law (KVL), Kirchhoff’s Current Law (KCL) is also just a simple concept (arguably even simpler than the KVL). It simply states that:
The sum of the currents in to a node are equal to the sum of the current going out of a node.
Alternatively represented as:
The algebraic sum of currents going into and out of a node are equal to zero.
This is easy to imagine using the analogy of water and forked pipes. Nodes are just the junctions between pipes.
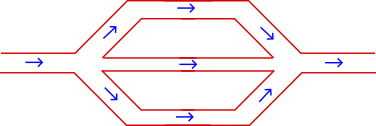
So it is intuitively obvious that the amount of water going in to the first node from the main pipe must be the same as the total volume of water that has split between the three pipes going out. Similarly it is common sense that the amount of water leaving in the output pipe must be the same as the combined water entering the pipe from the three feeding branches. It wouldn’t make sense to have more water coming out than went in.
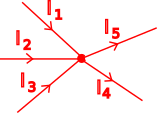
The same is true of electrical circuits. Since a node is effectively just point on a wire the current going into it must be equal to the current going out of it.
\(I_1 + I_2 + I_3 = I_4 + I_5\)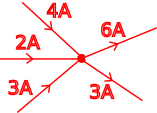
\(4A + 2A + 3A = 6A + 3A\)
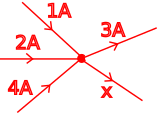
\(1A + 2A + 4A = 3A + x\) \(x = 1A + 2A + 4A – 3A\).
\(x = 4A\)
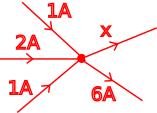
\(1A + 2A + 1A = x + 6A\) \(x = 1A + 2A + 1A – 6A\).
\(x = -2A\)
the minus in the answer means that we made an incorrect assumption about the direction of current flow for x. We phrased the equation as if x was an output, but the negative in the answer tells us that it is really an input. The answer is still valid, it just means that 2A is flowing into the node rather than out of it.