- What is electricity?
- Resistance, Conductance & Ohms Law
- Practical Resistors
- Power and Joules Law
- Maximum Power Transfer Theorem
- Series Resistors and Voltage Dividers
- Kirchhoff’s Voltage Law (KVL)
- Parallel Resistors and Current Dividers
- Kirchhoff’s Current Law (KCL)
- Δ to Y Network Conversion
- Y to Δ Network Conversion
- Voltage and Current Sources
- Thevenin’s Theorem
- Norton’s Theorem
- Millman’s Theorem
- Superposition Theorem
- Mesh Current Analysis
- Nodal Analysis
- Capacitance
- Series & Parallel Capacitors
- Practical Capacitors
- Inductors
- Series & Parallel Inductors
- Practical Inductors
Superposition Theorem
The Superposition theorem is a basic circuit analysis technique that is only useful where there are more than one voltage or current sources in the same circuit. It states that:
The current in any element is equal to the sum of currents through it produced by each source acting independently while the other sources are replaced by their internal resistance.
It is a basic technique that allows a circuit to be analysed using just one of the voltage/current sources at a time, Then summing the results by superimposing them on top of each other (hence the name). Generally such analysis is relatively straight forward and it is enough to use Ohms law and series/parallel circuit calculations to solve them.
Example 1
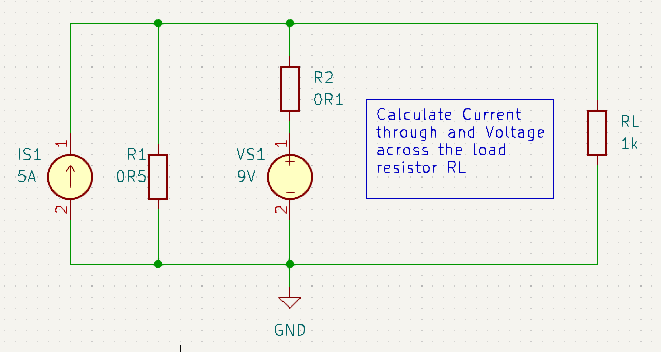
This circuit has two sources. A current source of 5A, with an internal resistance of 0.5Ω and a voltage source of 9V, with an internal resistance of 0.1Ω. So the steps to analyse this circuit will be:
- Find the current through RL based on IS1 being the only source, with VS1 represented only by it’s internal resistance.
- Find the current through RL based on VS1 being the only source, with IS1 represented only by it’s internal resistance.
- Sum the results to find the total current through the load resistor RL.
- Use Ohms law to calculate the voltage across RL based on the current calculated in step 3.
Step 1 – Find IRL contributed by IS1
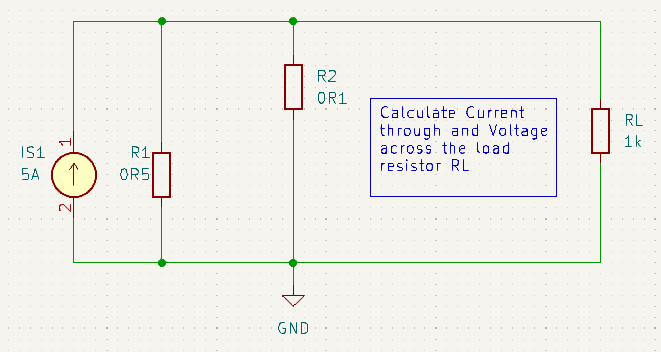
This is just a simple current divider calculation based on R1, R2 and RL
\(R_{Total} = \frac{1}{ \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}} = \frac{1}{ \frac{1}{0.5} + \frac{1}{0.1} + \frac{1}{1000}} = 0.0833\Omega \\\) \(I_{RL} = IS1 . \frac{R_{Total}}{R_L} = 5 * \frac{0.0833}{1000} = 0.0004166A \approx 417\mu A\)
Step 2 – Find IRL contributed by VS1
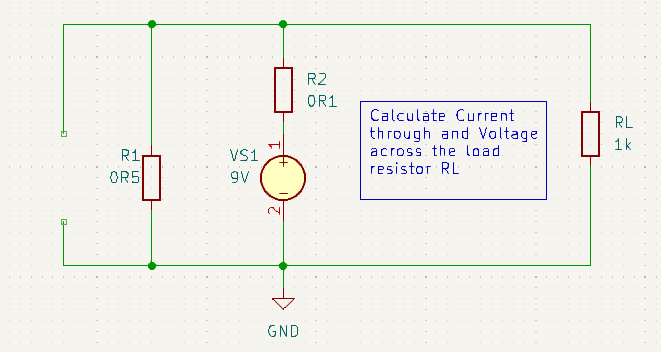
Redrawn to clarify the problem.
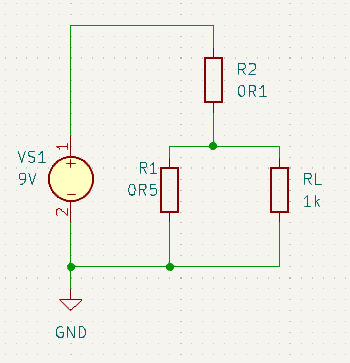
After redrawing the circuit to emphasise the connectivity of the resistor network we can see that this is only marginally more complicated than before. We can solve this by first finding the current through R2, then the fraction of that current through RL due to the current divider network of R1 || RL.
\(R_{Parallel} = \frac{R_1.R_L}{R_1 + R_L} = \frac{0.5 * 1000}{0.5 + 1000} = \frac{500}{1000.5} \approx 0.5\Omega \\\) \(I_{R2} = \frac{VS_1}{R_2 + R_{Parallel}} = \frac{9}{0.1 + 0.5} = 15A\\\) \(I_{RL} = I_{R2} . \frac{R_{Parallel}}{R_L} = 15 * \frac{0.5}{1000} = 0.0075A \approx 7.5mA\)
Step 3 – Sum results to Find IRLTotal
\(IRL_{Total} = IRL_{IS1} + IRL_{VS1} = 0.000417 + 0.0075 = 0.007917A \approx 7.9mA\)
Step 4 – Calculate VRL
\(V_{RL} = IRL_{Total} . RL = 0.0079 * 1000 = 7.9V\)
Summarising
IRL = 7.9mA and VRL = 7.9V
xx